5.0 The RSA Algorithm
The Rivest-Shamir- Adelman(RSA) scheme has since that time reigned supreme as the most widely accepted and implemented general purpose approach to public key encryption.
The RSA scheme is a block cipher in which the plain text and cipher text are the integer values between 0 to n-1 for some n. A typical size for n is 1024 bits, or 309 decimal digits.
The encryption and decryption are of the following form, for some plain text block M and cipher text block C:
The RSA scheme is a block cipher in which the plain text and cipher text are the integer values between 0 to n-1 for some n. A typical size for n is 1024 bits, or 309 decimal digits.
The encryption and decryption are of the following form, for some plain text block M and cipher text block C:
C = Me mod n
M = Cd mod n
Both sender and receiver must know the value of n. the sender knows the value of e, and only the receiver knows the value of d, thus, this is a public key encryption algorithm with a public key of KU = {e, n} and a private key of KR = {d, n} . For this algorithm to be satisfactory for public key encryption, the following requirements must be met:
1. It is possible to find values of e, d , n such that Med = M mod n for all M< n.
2. It is relatively easy to calculate Me and Cd for all values of M<n.
3. It is infeasible to determine d given e and n.
Key Generation | |
Select p , q | p and q both prime, p ≠ q |
Calculate n=p × q | |
Calculate f(n) = (p-1) × (q-1) | |
Select integer e | gcd(f(n) , e) = 1; 1 < e < f(n) |
Calculate d | d = e-1 mod f(n) |
Public key | KU = {e , n} |
Private key | KR = {d , n} |
Encryption | |
Plaintext | M < n |
Cipher text | C = M e (mod n) |
Decryption | |
Cipher text | C |
Plaintext | M = C d (mod n) |
Figure:- RSA algorithm
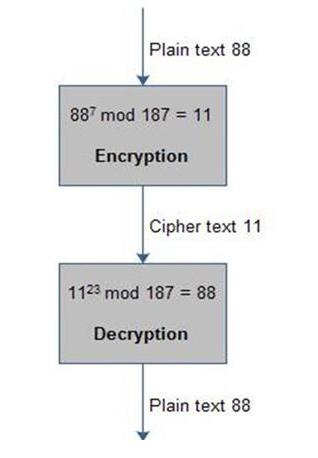
Example:
>> Select two prime numbers p = 17 and q = 11.
>> Calculate n = pq = 17 ×11 = 187.
>> Calculate f(n) = (p - 1)(q - 1)
= 16× 10 = 160.
>> Select e such that e is relatively prime to f(n) = 160 and less than f(n) ;
We choose e = 7.
We choose e = 7.
>> Determine d such that de =1 mod 160 and d < 160.
The correct value is d = 23;
The correct value is d = 23;
>> KU = ( e , n ) = (7,187)
>> KR = ( d , n ) = (23,187)
Figure:- Example of RSA algorithm
5.1 The Security of RSA
Three possible approaches to attacking the RSA algorithm are as follows:
>> Brute force: This involves trying all possible private keys.
>> Mathematical attacks: these are several approaches, all equivalent in effect
to factoring the product of two primes.
>> Timing attacks: These depends on the running time of the decryption algorithm.